Buchstabenrechnung

Buchstabenrechnung, keine eigene Rechnungsart, sondern blos eine Methode, bes. Fälle auf eine allgemeine Weise auszudrücken. Um dies zu können, mußte man allgemeine Zeichen wählen, u. zwar nahm man die kleinen lateinischen Buchstaben, weil diese sich am bequemsten schreiben lassen u. bes. weil sie am weitesten verbreitet sind. Sie können jede Art von Größen bezeichnen, also auch geometrische Größen, Kräfte, Zeiten, Geschwindigkeiten. In einer u. derselben Rechnung jedoch bedeutet derselbe Buchstabe dieselbe Größe. Die B. ist wichtig wegen der größten Allgemeinheit, die durch sie erreicht wird, u. weil man. da die Rechnungen nur angedeutet werden können, jeder zusammengesetzten Größe sogleich ansehen kann, auf welche Art sie aus ihren Theilen zusammengesetzt ist. In der ganzen Analysis bedient man sich der B. Im engeren Sinne versteht man unter B. die 4 Grundspecies. Über diese läßt sich im Allgemeinen sagen, daß sie durch die 4 Rechnungszeichen od. bei der Multiplication durch bloße Zusammenstellung der Buchstaben nur angedeutet, aber nicht ausgeführt werden können, wenn die Buchstaben nicht mit bestimmten Größen verbunden sind; haben sie dagegen bestimmte Größen vor sich stehen (man schreibt diese vor die Buchstaben u. nennt sie Coefficienten), so läßt sich die Rechnung theilweise ausführen. a) Addition: Soll man gleichnamige Buchstaben ausdrücken, d.h. solche, in denen dieselben Buchstaben auf dieselbe Art verbunden sind, so addirt man ihre Coefficienten u. erhält so den neuen Coefficienten des unveränderten Buchstabenausdruckes, z.B.: 4 (a + b) + 12 (a + b) = 16 (a + b). b) Subtraction: Dasselbe gilt hier, man führt die Rechnung nur an den Coefficienten aus, also: 12 (a + b) – 4 (a + b) = 8 (a + b). c) Multiplication: Hier multiplicirt man die Coefficienten u. schreibt ihr Product als neuen Coefficienten dem Producte der Buchstaben vor, das man alphabetisch ordnet, z.B.: 5 ab. 2 ce. 3 df = 30 abcdef. Sind die Factoren gleichnamig, so werden sie potenzirt (s. [418] Potenz), z.B.: aaaa = a⁴ die 4 heißt der Exponent. Sollen gleichnamige Buchstabenausdrücke, welche Exponenten haben, multiplicirt werden, so addirt man ihre Exponenten, z.B.: 5 a³ b⁴c. 3 a² b d³ = 15 a⁵ b⁵ cd³. Sind die Factoren zusammengesetzt, so muß man jedes Glied des einen einzeln nach den angegebenen Regeln mit jedem des anderen multipliciren u. dabei der besseren Übersicht wegen stets die alphabetische Reihenfolge der Buchstaben u. der einzelnen Glieder vor Augen haben. d) Division: Bei ungleichnamigen Ausdrücken kann die Rechnung ebenso nur an den Coefficienten ausgeführt werden, haben Divisor u. Dividend, od. Zähler u. Nenner (denn man schreibt gewöhnlich gleiche u. ungleiche Buchstaben in Bruchform), so gehen erstere heraus, die letzteren bleiben, z.B.:

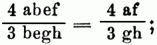
sind alle gleichnamig, so verschwinden die Buchstaben ganz, z.B.:

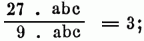
haben die Buchstabenausdrücke, Exponenten, so müssen diese von einander subtrahirt werden, außerdem gilt das Übrige, z.B.:

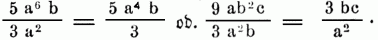
Sind Divisor u. Dividend zusammengesetzte Ausdrücke, so müssen sie zunächst alphabetisch geordnet werden, u. dann dividirt man nach den angegebenen Regeln mit jedem Gliede des Divisors der Reihe nach die einzelnen Glieder des Dividendus, wie man es mit bestimmten Größen thut, z.B.:

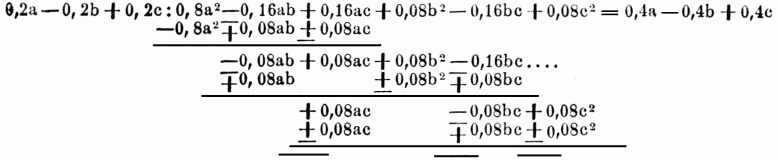
Borrel führte zuerst in der Mitte des 16. Jahrh., statt der früheren willkührlichen Zeichen der unbekannten Größen, große Buchstaben ein; Wiete wählte dann zu Ende des 16. Jahrh. auch für die bekannten Größen (statt der Zahlen) große Buchstaben; Th. Harriot setzte an deren Stelle zu Anfage des 17. Jahrh. kleine Buchstaben. Cartesius führte die noch jetzt allgemein herrschende Sitte ein, für die bekannten Größen die ersten Buchstaben des Alphabets, abc, für die unbekannten die letzten, xyz, zu gebrauchen; zugleich bezeichnete er die Dignitäten mit den Exponenten a² a³ etc.; Newton u. Leibnitz aber führten unbestimmte Exponenten ein, wo man statt der Zahlen auch Buchstaben, u. zwar mittlere, m n p, wählt. In neuerer Zeit werden große Buchstaben nur zur Bezeichnung bes. merkwürdiger Größen zur Abkürzung gebraucht. Die erste umfassende Darstellung der B. ist von Bartholin in Principia matheseos univ.