Cotesischer Lehrsatz

Cotesischer Lehrsatz, Lehrsatz nach dem Mathematiker Roger Cotes benannt, zeigt, wie eine Function von der Form aⁿ 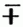xⁿ vermittelst folgender Eigenschaft des Kreises in zwei- od. dreigliedrige Factoren zerlegt werden könne. Theilt man die Peripherie eines aus C mit einem Halbmesser = a beschriebenen Kreises in den Punkten M, M₁, M₂, M₃. in 2_n gleiche Theile u. wählt auf dem durch den Anfangspunkt M gehenden Durchmesser einen Punkt O, dessen Abstand vom Mittelpunkt c = x sei, so ist, wenn man aus O nach allen Theilungspunkten Gerade zieht, das Product aus allen, nach einem geradzahligen M gezogenen Linien, d. i. OM × OM₂ × OM₄ ... × OM_2n – ₂ = aⁿ – xⁿ, wenn O innerhalb des Kreises u. = xⁿ – aⁿ, wenn O außerhalb desselben in der Verlängerung des durch M gehenden Durchmessers liegt; endlich das Product aus allen von O nach einem ungeradzahligen M gezogenen Linien, d. i. OM₁ × OM₃ × OM₅ ... OM_2n – ₁ = aⁿ + xⁿ. Nun ist ein beliebiger nach M_k gezogener Strahl OM_k = √ x² – 2ax cos ^k/_n π + a²), u. da ihm bei der geraden Anzahl der Theilpunkte ein gleicher Strahl OM_{2n k} im anderen Halbkreis entspricht, so ist OM^k OM_2n – _k = x² – 2ax cos^k/_nπ + a². Hieraus geht aber hervor, daß aⁿ + xⁿ, sowie auch aⁿ – xⁿ gleich einem Producte mehrerer Factoren ist, die im Allgemeinen die Form xⁿ – 2ax cos ^k/_nπ + a² haben, unter denen aber der erste, wenn n eine ungerade Zahl ist, x – a heißt. Von diesem in Cotes Harmonia mensurarum (Canterb. 1722) ohne Beweis zuerst mitgetheilten Satze geben Beweise Bernoulli, Klügel u. Lacroix. Moivre, von dem es ebenfalls einen Beweis dieses Satzes gibt, dehnte letzteren auf alle Functionen von der Form a²ⁿ – 2aⁿ xⁿ cos φ + x²ⁿ aus, u. von ihm nennt man ihn den Moiverschen Lehrsatz. Beide dienen zur Bestimmung der Wurzeln einer Gleichung.