Gammafunction

Gammafunction. Die Definition der G. ist gegeben durch die Gleichung

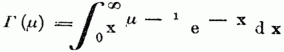
Die Eigenschaften dieses, weder algebraisch, uoch durch die Transcendenten, für welche man schon bisher Tafeln besaß, also durch Logarithmen od. trigonometrische Functionen, ausdrückbaren u. daher als eine neue transcendente Größe zu betrachtenden Integrals sind zuerst von Euler untersucht worden, daher es auch von Legendre neben einem andern damit verwandten Integral, als die Eulersche Transcendente (Eulersches Integral) der zweiten Art bezeichnet worden ist. Von Legendre rührt auch die Bezeichnung durch den Buchstaben Γ her, so wie er u. Gauß den Algorithmus dieser Transcendenten umfassend bearbeitet haben. Aus der obengenannten Gleichung, welche sich auch so umformen läßt:

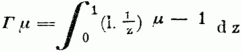
folgt durch Integration Γ (μ + 1) = μΓ (μ) u. da der Definition gemäß Γ(1) = 1 ist, so ist nun Γ(2) = 1. 1, Γ (√3) = 1.2, Γ (μ) = 1.2. 3... (μ – 1) u. wenn m eine ganze Zahl ist

Γ (μ + m) = μ (μ + 1) (μ + 2).. (μ + m – 1) Γμ

Hieraus ersieht man, daß Γ(μ)) für jeden Werth von μ berechnet werden kann, wenn man es für alle echt gebrochenen μ kennt, da jede Zahl sich in eine ganze Zahl u. einen ächten Bruch zerlegen läßt. Zunächst ist es nun nicht schwer für μ = ¹/₂ den zugehörigen Werth der G. zu finden. Nach Gauß ist nämlich die zu Anfange angeführte Gleichung identisch mit folgender

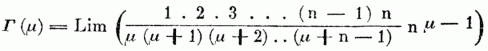
für ins Unendliche wachsende u. Aus ihr folgt weiter

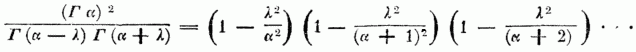
u. für α = 1

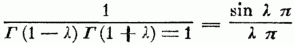
also da Γ (1_– λ) = λ Γ (λ) ist

ΓλΓ(1_– λ) = ^π/_sinλπ

Setzt man hierin λ = ¹/₂, so ist

Γ(¹/₂) = √π

Nach Annäherungsformeln, welche hier nicht näher angegeben werden können, haben Legendre u. Gauß auch für alle übrigen echten Brüche Tafeln der Function ((Γ)μ) berechnet, welche bei der Berechnung vieler bestimmter Integrale, sowohl in rein analytischen Untersuchungen, als auch in Anwendungen, z.B. auf die Theorie der Verbreitung der Wärme, von großer Bedeutung sind.