Cardans Regel

Cardans Regel, nach Cardano 1) benannte Methode der Auflösung cubischer Gleichungen. Die allgemeine Form einer solchen ist nämlich y³ + ay² + by + c = o; indem man jedoch hierin für y den Ausdruck x –¹/₃ a einsetzt, verschwindet das Glied, welches die zweite Potenz der Unbekannten enthält, u. die Gleichung gewinnt die Form x³ + mx + n = o; die Wurzel dieser letzteren aber ist

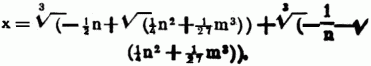
[687] Diese Formel heißt die Cardanische Formel. Nach Cardanos eigenem Geständnisse gebührt Scipio Ferreus von Bologna der Ruhm, die Auflösung der Gleichung: x³ + mx = n um 1505 gefunden zu haben. Sein Schüler Florido reizte durch Aufgaben, die auf diese Gleichung führten, Tartalea aus Brescia, der schon früher zwei andere cubische Gleichungen aufgelöst hatte, zum weiteren Nachforschen. Er fand, außer der Florido bekannten, noch die für x³ = mx + u. Auf Cardanos inständiges Bitten theilte Tartalea diesem Freunde die Auflösung, jedoch ohne Beweis, mit. C. machte sie u. den Beweis derselben in seiner Ars magna gegen sein Versprechen bekannt, worüber er mit Tartalea in Streit gerieth. Die in der Cardanischen Formelvorkommende Quadratwurzel √ (1/4n² + 1/27m³) wird in vielen Fällen imaginär, obwohl dann gerade alle die Wurzeln der Gleichung reell sind. Dieser Fall heißt Casus irreducibilis. Doch läßt sich auch dann die Formel noch zur Auffindung der Wurzel anwenden, indem man ihre beiden Kubikwurzeln nach dem binomischen Lehrsatze im Rechen entwickelt, wobei alle Glieder mit dem Factor √–1 verschwinden; od. auch indem man für

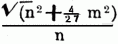
die trigonometrische Function tg φ einführt, wodurch der Kubikfuß sich auf den reellen Ausdruck

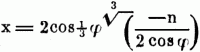
reducirt.