- Rösselsprung
Rösselsprung, der Sprung des Rössels (Springers) auf dem Schachbrete, welcher darin besteht, daß die Figur zwei Felder gerade aus geht u. dann auf das nächste Feld zur linken od. rechten Seite gestellt wird. Die Rösselsprungaufgabe hat man diejenige Aufgabe genannt, von irgend einem Felde des Schachbretes beginnend im R. sämmtliche Felder zu berühren, ohne daß eins derselben mehr als einmal berührt wird. Es scheint bloße Spielerei, ist aber eine Aufgabe der Analysis der Lage. Euler hat sich bes. damit beschäftigt u. mehre Auflösungen in den Mémoires de l'Académie de Berlin, T. XV., année 1759 geliefert. Die einfachste ist: Man sondere innerhalb der 64 Felder des Schachbretes ein mittleres Quadrat von 16 Feldern ab, so daß ringsherum eine Einfassung von zwei Streifen Feldern bleibt. In je zwei neben einander liegenden Streifen kann der Springer (das Rössel) 4 Schritte u. in der ganzen Einfassung 12 Schritte thun, u. nach jeden 12 Schritten bleibt ein Gang in das innere Quadrat offen. In diesem kann er je 4 Schritte thun u. nach je 4 Schritten bleibt ein Gang in die Einfassung frei. Auf solche Art wird der Springer richtig durch alle 64 Felder geführt. Also in der Weise, wie die Zahlen von 1–64 auf
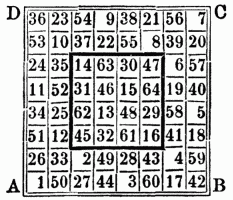
Die Zahlen 1_... 12 u. 17_... 28 folgen nach der Ordnung der Ecken A B C D auf einander; die Zahlen 33_... 44 u. 49_... 61 nach der entgegengesetzten A D C B. Im inneren Quadrat folgen allein die Zahlen 29_... 32 nach der Ordnung A B C D; die Zahlen in den Feldern des inneren Quadrats bilden systematisch je vier theils ein rechtwinkliches, theils ein verschobenes gleichseitiges Viereck. Vgl. Berliner Schachzeitung 1849–50. Die Rösselsprungaufgabe hat man in neuerer Zeit auch dazu benutzt, um Gedichte od. Verse in die 64 Felder so zu vertheilen, daß während das erste Wort des Gedichtes von irgend einem beliebigen Felde an beginnt u. jedes folgende Wort (od. Worttheil) nach Art des R-s weiter springt, endlich alle Felder ausgefüllt werden. Die Reihenfolge der Worte aufzufinden u. somit das Gedicht selbst zu erhalten, ist hier die zu lösende Aufgabe.
Pierer's Lexicon. 1857–1865.
