Magisches Quadrat

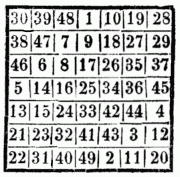
Magisches Quadrat, 1) ein in gleiche Fächer eingetheiltes Quadrat, worin Zahlen einer Folgereihe so eingetragen sind, daß ihre Summen in jedem horizontalen u. jedem perpendiculären Streifen, eben so aber auch längs jeder Diagonale, gleich groß sind. Ihr Ursprung scheint in Indien zusein, von wo sie zu den Arabern, von diesen aber nach Europa gelangten. Ihre Benennung haben sie von der Anwendung, die man sonst von ihnen als Talismanen machte; vgl. auch Planetenspiegel. Em. Moschopulos (um 1400) ist der erste, der über sie geschrieben hat (in einem Manuscripte auf der königlichen Bibliothek in Paris), Agrippa von Nettesheim aber der erste, der (De occulta philosophia) ihrer erwähnt. Am leichtesten darzustellen sind die mit ungeraden Seitenzahlen. So gibt die Seitenzahl 7, in allen seinen (7 horizontalen, 7 verticalen u. zugleich 2 mittlern Diagonalen) Reihen die Zahl 175.

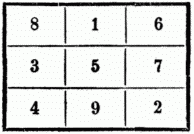
Das einfachste aber u. auch als Planetensiegel gewöhnlichste, mit der Seitenzahl 3, wo dann der summarische Betrag 15 ist, stellt nach derselben Construction sich in folgender Art dar

Eben so kann man von dem untersten mittlern Fach, das hier mit der höchsten Zahl erfüllt ist, anheben, hier die 1 einzeichnen u. in alle, aber in entgegengesetzter diagonaler Richtung wie dort, die Zahlen einzeichnen u. verrichten gleichen Zweck. Für Quadrate mit gleichen Seitenzahlen fertigt man am einfachsten zuerst ein Quadrat nach der natürlichen Folgenreihe der Zahlen an, indem man die Fächer der Horizontalreihen von oben nach unten (od. auch von unten nach oben damit ausfüllt); dann aber versetzt man in einem zweiten Quadrate die Hälfte der Zahlen jeder obern Reihe mit eben so vielen der entsprechenden untern Reihe (der ersten u. der letzten, der zweiten u. der vorletzten untern) aber aus entgegengesetzten verticalen Reihen, so daß die Summe der versetzten Zahlen der Summe der höchsten Zahl mit Zufügung von 1 gleich ist. Beispiel:

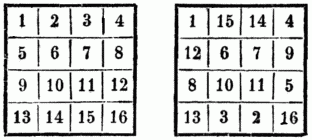
Die Summe sämmtlicher Reihen ist hier 34, u. die Summe jeder versetzten mit der ihr entsprechenden bleibenden Zahl 17 Für die größern Quadrate dieser Art, bes. auch, je nachdem sie Seitenzahlen haben, die bis auf zwei, od. solche, die nur bis auf eine höhere, ungleiche Zahl zerlegt werden können, gibt es, hinsichtlich der zu bewirkenden Versetzungen, besondere Anweisungen. Nur das M. Q. mit. der Seitenzahl 3 ist keiner wesentlichen Abänderung unterworfen. Dagegen läßt schon das M. Q. mit der Seitenzahl 4880 verschiedene Abänderungen zu. Bei noch größern Quadraten aber wächst die Summe der möglichen Abänderungen für jede folgende Seitenzahl nach ungemein großen Zahlenverhältnissen. Es lassen überhaupt diese sich so einrichten, daß man die äußeren Reihen wegnehmen kann u. doch noch ein M. Q. bleibt, also als. M. Q-e mit magischen Einfassungen; od. es können auch M. Q-e mit symmetrischen Abtheilungen construirt werden, z.B. ein neunseitiges, das in 9 dreiseitige sich zerlegen läßt (wovon das erste die Zahlen 1–9 enthält, ein zweites die Zahlen 10–18 etc.). Hieraus[702] erhellt die ungemeine Mannigfaltigkeit, mit der sich solche größere Quadrate nach den gegebenen Bedingungen construiren lassen. So ist. ein M. Q. mit der Seitenzahl 6 u. magischer Einfassung nicht weniger als 84,155,840 Veränderungen unterworfen, das mit der Seitenzahl 7 sogar 4,777,574,406 Mal zu verändern. Man kann auch, statt einer arithmetischen Progression, eine geometrische in die Fächer eines Quadrats so eintragen, daß das Product der Zahlen in den Horizontal-, Vertical- u. Diagonalreihen dasselbe ist. Beispiel, welchem die geometrische Progression 1,2,4,8 etc. zu Grunde liegt:

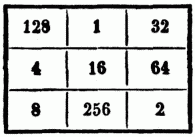
Vgl. Mollweide, De quadratis magicis, Lpz. 1816. G. Hohndell, Praktische Anleitung zur Bildung u. Berechnung magischer od. sogenannter Zauberquadrate, Lpz. 1837. 2) (Ästh.). Zusammenstellung von Buchstaben, die in jeder Versetzung einen Sinn geben, in verticalen wie in horizontalen Reihen, wie:

wo die vier mit denselben Buchstaben geschriebenen Worte dieselben sind, wenn man sie auch in verticaler Reihe liest; gehört zu den Wort- od. auch Räthselspielen.