- Zusammengesetzte Proportionsrechnung
Zusammengesetzte Proportionsrechnung, der Inbegriff der Regeln für die Berechnung einer Größe x, deren Verhältniß zu einer bekannten Größe derselben Art aus den Verhältnissen mehren anderen bekannten Größen zusammengesetzt ist. Sind 5 Größen bekannt u. x die 6., so erhält man eine Aufgabe der sogen. Regel quinque, sind 7 bekannt der Regel septem, sind noch mehr bekannt, die Regula multiplex. Diese Benennungen finden sich noch in den älteren Rechenbüchern, kommen aber immer mehr ab. Die Aufgabe theilt sich in einen bekannten Satz u. einen Fragesatz, in letzterem kommt eine unbekannte Größe x vor, in ersterem eine ihr gleichbenannte gegebene Größe g; außerdem befinden sich in beiden Sätzen je zwei gleichbenannte Größen, welche entweder in directem od. umgekehrtem Verhältniß der Größen g u. x stehen; dies letztere erkennt man daran, ob die Größe von der Benennung von g u. x zugleich mit jenen Größen wächst od. abnimmt, während jene wachsen. Multiplicirt man nun das Product sämmtlicher gegebener Verhältnisse od. resp. ihre Umkehrungen mit g, so erhält man x. Z. B. ein Erdwall 7 (= a) Fuß hoch, 17 (= b) F. breit, wird 93 (= c) Schritt weit abgekarrt; es arbeiten daran 13 (= d) Mann täglich 10 (– e) Stunden u. vollenden in 19 (=f) Tagen eine Wallstrecke von 21 (= g) Ruthen Länge. Wenn nun an einen ähnlichen Wall von 5 (=a) F. Höhe, 14 (=b') F. Breite, welcher 97 (= c') Schritt weit abgekarrt wird, 18 (=d') Arbeiter täglich 11 (= e') Stunden beschäftigt sind, wie groß wird die von ihnen in 23 (=f') Tagen abgetragene Länge (=x) sein?[753] Bekannter Satz: a Höhe b Breite c Schritt d Mann e Stunden f Tage g Ruthen.
Fragesatz: a' – b' – c' – d' – e' – f' – x-
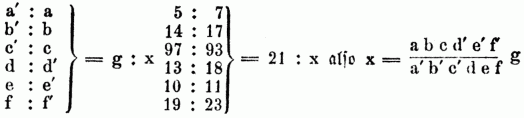
Noch einen anderen Ansatz erhält man nach der Reesischen Regel. Man stelle x zur Linken eines verticalen Striches u. unter dasselbe diejenigen Größen des Fragesatzes, mit deren Wachsen es abnimmt, zur Rechten stellt man tiefer die übrigen Größen der Frage. Zuletzt schreibt man neben jeder dieser Zahlen die gleichartige aus der Angabe hin u. erhält so folgendes Schema:

Nachdem man, je nachdem es nöthig, reducirt, die Brüche fortgeschafft u. gehoben hat, dividire man das Product aller Größen rechts durch das aller links u. erhält in der Benennung von x das Resultat. Gergonne gibt folgende Regel an: Man bilde aus den Gliedern jedes der vollständigen Verhältnisse einen Bruch u. multiplicire das Product dieser Brüche mit dem gegebenen Gliede des unvollständigen Verhältnisses, so erhält man das zu diesem gehörige fehlende Glied x. Um nun zu bestimmen, welches Glied jedes Verhältnisses den Zähler bildet, untersuche man successiv, ob unter der Voraussetzung, daß jede der gegebenen Zahlen des Fragesatzes zu 0 wird, die gesuchte Zahl zu Null od. unendlich groß wird. Im ersten Falle wird die gegebene Zahl des Fragsatzes Zähler, im zweiten Nenner des Bruches. Dies auf unser Beispiel angewandt gäbe a/a', b/b', denn hatte der Wall keine Höhe od. Breite, so würde ein unendlich großes Stück abgetragen werden können; c/c' denn würde die Erde nicht fortgeschafft, so würde unendlich viel abgetragen werden können; d'/d, denn würde kein Arbeiter arbeiten, so würde auch nichts abgetragen etc., man bekommt also x = a/a' ._ b/b' ._ c/c' ._ d/d' ._ e/e' ._ f'/f ._ g dasselbe, was der erste Ansatz kehrte.
Pierer's Lexicon. 1857–1865.
