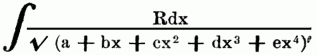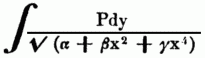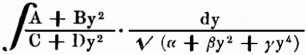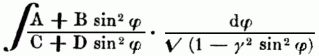Elliptische Functionen

Elliptische Functionen

Elliptische Functionen (Elliptische Transscendenten), Functionen, deren Integrale von der Länge elliptischer Bogen abhängen, die bei gegebenen Halbachsen einer gewissen Abscisse entsprechen. Sie sind alle begriffen in dem Integrale:

Elliptische Functionen

worin R eine rationale Function von x ist u. a, b, c, d, e constante reelle Größen bezeichnen. Dies Integral läßt sich nach Legendre auf jenes

Elliptische Functionen

[652] so wie dieses auf das

Elliptische Functionen

u. endlich dieses auf die Form

Elliptische Functionen

zurückführen. Daher theilt Legendre die E. F. in 3 Gattungen, nämlich, wenn man mit ihm √ (1 – γ2 sin2φ) = Δ setzt, in

F = ∫ dφ/Δ E = ∫ Δdφ und Π = ∫ dφ/[(1 + n2sin2φ)Δ].

Die ersten Arbeiten über diesen Gegenstand lieferten Fagnani (1718), Landen, Lagrange u. Euler; Legendre prüfte jene Forschungen u. erweiterte sie; Jacobi (Nova theoria functionum ellipticarum, Königsb. 1829) u. Abel bildetendiese Lehre weiter aus.


Pierer's Lexicon. 1857–1865.

Игры ⚽ Поможем сделать НИР

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Jacobische elliptische Funktion — In der Mathematik ist eine Jacobische elliptische Funktion eine von zwölf speziellen elliptischen Funktionen. Die Jacobischen elliptischen Funktionen haben einige Analogien zu den trigonometrischen Funktionen und finden zahlreiche Anwendungen in… …   Deutsch Wikipedia

  • Heinrich Weber (Mathematiker) — Heinrich Martin Weber (* 5. März[1] 1842 in Heidelberg; † 17. Mai 1913 in Straßburg) war ein deutscher Mathematiker. Inhaltsverzeichnis 1 Leben 2 Werk 3 Publikat …   Deutsch Wikipedia

  • Эллиптические интегралы и функции — Э. интегралами называются все квадратуры вида: ∫ f(x,√ X)dx, где Х есть какой либо многочлен (полином) третьей или четвертой степени от х; f есть какая либо рациональная функция от х и √X. Все такие интегралы могут быть выражены в интегралах… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

  • Ellipse — (v. gr.), 1) Gramm.), Auslassung eines, zur Vollständigkeit eines Satzes nothwendigen, jedoch durch den Zusammenhang leicht zu ergänzenden Redetheiles. Die E. findet meist in, durch den Sprachgebrauch üblich gewordenen Redensarten, bes. in… …   Pierer's Universal-Lexikon

  • Сохоцкий Юлиан Васильевич — Сохоцкий (Юлиан Васильевич) ординарный профессор математики в Санкт Петербургском университете, родился в 1842 г. Начальное образование получил в варшавской губернской гимназии; университетский курс прослушал в Санкт Петербурге. Наиболее важные… …   Биографический словарь

  • Сохоцкий, Юлиан Василевич — ординарный профессор математики в спб. университете; родился в 1842 г. Начальное образование получил в варшавской губернской гимназии; университетский курс прослушал в С. Петербурге. Наиболее важные работы: "Теория интегральных вычетов с… …   Большая биографическая энциклопедия

  • Eduard Study — (March 23, 1862 ndash; January 6, 1930) was a German mathematician known for work on invariant theory of ternary forms (1889) and for the study of spherical trigonometry. He is also know for contributions to space geometry, hypercomplex numbers,… …   Wikipedia

  • Сохоцкий — (Юлиан Василевич) ординарный профессор математики в спб. университете, родился в 1842 г. Начальное образование получил в варшавской губернской гимназии; университетский курс прослушал в С. Петербурге. Наиболее важные работы: Теория интегральных… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

  • Christian Hugo Eduard Study — Eduard Study Eduard Study, genauer Christian Hugo Eduard Study (* 23. März 1862 in Coburg; † 3. Januar 1930 in Bonn) war ein deutscher Mathematiker. Study leistete unter anderem bedeutende Beiträge zur Invariantentheorie ternärer Formen, zu… …   Deutsch Wikipedia

  • Eduard Study — Eduard Study, genauer Christian Hugo Eduard Study (* 23. März 1862 in Coburg; † 6. Januar 1930 in Bonn) war ein deutscher Mathematiker. Study leistete unter anderem bedeutende Beiträge zur Invariantentheorie ternärer Formen, zu hyperkomplexen… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”