Sectĭo

Sectĭo (lat.), 1) eigentlich das Schneiden, Einschneiden, Schnitt; so: S. caesarĕa, s. Kaiserschnitt. S. hypogastrĭca, der hohe Steinschnitt u. S. laterālis, der Seitensteinschnitt, s.u. Steinschnitt. S. legalis, s. Section, vgl. Obduction. S. musculorum, s. Tenontotomie. S. ossium pubis, s. Synchondrotomie. S. renalis, s. Nierenschnitt. S. tendĭnum, s. Tenontotomie. S. vesicalis, Blasenschnitt, s. Steinschnitt. S. viva, Vivisection, s.d. 2) Zerschneiden; so S. anatomica, die Leichenzergliederung, s. Section; 3) Vertheilung, bes. der Kriegsbeute; 4) (S. bonorum), in Rom die öffentliche Verkaufung der Güter dessen, welcher innerhalb 60 Tagen seinem Gläubiger nicht Zahlung leisten konnte; od. solcher Güter, welche dem Staat anheimgefallen waren, später auch, wenn eine dem Fiscus zugefallene Erbschaft versteigert wurde; der Käufer solcher Güter hieß Sector; 5) Auction; 6) der Gegenstand, welcher verauctionirt wird; 7) (Math.), so v.w. Durchschnitt, s.d. 1). Auch Name mehrer geometrischer Aufgaben, so: S. aurĕa (S. divīna), von Euklides gelöste Aufgabe: auf einer begrenzten Geraden einen Punkt von der Beschaffenheit zu finden, daß das Quadrat über seinem Abstande von einem der Endpunkte gleich werde dem Rechteck aus seinem Abstande vom anderen Endpunkte der Geraden in die Gerade selbst. Man beschreibt mit der gegebenen Linie m n als Halbmesser aus n einen Kreis, verlängert m n zum Durchmesser m p, zieht auf diesen einen Radius n o senkrecht, halbirt den Halbmesser n p in q u. schneidet auf q m ein Stück q r = q o ab, so ist r der gesuchte Punkt, es ist rn° = mn : mr. Weil diese Gleichung als Proportion geschrieben, diese Form: m n : r n = r n : mr hat, so nennt dies Euklides die Theilung der Geraden nach den äußeren u. mittleren Verhältnissen. Die Aufgabe, ein reguläres Fünf- od. Zehneck zu construiren, u. anderes damit in Verbindung Stehende reducirt sich auf diese Auflösung. Wegen dieser vielfachen Anwendbarkeit hat sie später ihren Namen erhalten. S ratiōnis, Aufgabe: auf jeder von zwei durch den Winkel 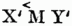, welchen sie mit einander bilden, der Lage nach gegebenen Geraden XX' u. YY' ist A u. B gegeben; man soll durch einen dritten ebenfalls gegebenen Punkt Q derselben Ebene eine Gerade OP so legen, daß die dadurch entstehenden Abschnitte AO u. BP auf den Linien AX' u. BY', welche von den gegebenen Punkten u. der dritten Geraden begrenzt werden, in einem gegebenen Verhältnisse stehen, daß OA: PB = 1 : m. Zieht man durch Q die Parallelen QD zu XX' u. QC zu YY' u. setzt MA = a, MB = b, MC = c, MD = d, BP = y, also AO = (¹/_m) y, so ergibt sich die Auflösung der Aufgabe in allen Fällen aus der quadratischen Gleichung: y² – (m [a + c] + b + d) y + m (ab + ad + bc) = o; hierbei werden a u. c, b u. d nach entgegengesetzten Seiten als positiv gerechnet. Nach der bei den Alten üblichen rein geometrischen Behandlungsweise erforderte jedoch jeder besonderer Fall seine eigene, mehr od. weniger von den übrigen abweichende Auflösung. Diese Aufgabe ist der Gegenstand der Schrift Περὶ λόγου ἀποτομῆς des Apollonios (s.d. 5) Pergäos; sie ist ferner enthalten in G. Paukers Geometrischer Analysis, Lpz. 1837. S. spatii, eine mit der S. rationis verwandte, ebenfalls von Apollonios behandelte Aufgabe, welche Halley nach des Pappus Mittheilungen (in seiner Schrift De sectione rationis) u.a. Richter (in des Apollonios zwei Büchern vom Raumschnitt, Halberst. 1828) wiederherzustellen versucht hat. Wenn bei der S. rationis die Abschnitte AO u. BP ein gegebenes Verhältniß haben sollen, so soll hier das Rechteck aus diesen Abschnitten einer gegebenen Fläche gleich sein. Vgl. G. Pauker, Geometrische Analysis, Lpz. 1837.