Seilpolygon

Seilpolygon, Polygon, welches von einem, im Gleichgewichte sich befindenden biegsamen, in beliebig vielen Punkten durch Kräfte nach beliebigen Richtungen gespannten Faden gebildet wird. Gewöhnlich vereinfacht man die Aufgabe, die Bedingungen des Gleichgewichts bei einem S. zu finden, dahin, daß man einen unelastischen Faden ohne Schwere voraussetzt. An den beiden Endpunkten des Seils wirken nach der Richtung desselben die Kräfte A u. A' u. in beliebig viel anderen Punkten die Kräfte P₁, P₂, P₃...; die Richtungen dieser Kräfte auf den 3 Achsen eines rechtwinklichen Coordinatensystems seien resp. (a, b, c), (a', b', c'), (α1, β1, γ1), (α2, β2, γ2), (α3, β3, γ3),....., so müssen alle am S. angebrachten Kräfte von der Art sein, daß sie, parallel mit sich fortgetragen u. an einem u. demselben Punkte angebracht, sich das Gleichgewicht halten müssen. Dies gibt die drei Gleichungen

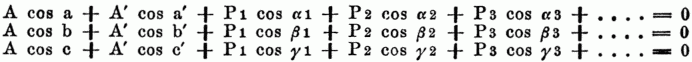
Am häufigsten kommt der Fall vor, daß die Kräfte P₁, P₂, P₃,.... herabhängende Gewichte sind; dann liegt das S. in einer Ebene u. man hat nur zwei Gleichungen nöthig; nimmt man außerdem die eine der Coordinatenachsen parallel der verticalen Richtung, so werden α1 α2 α3... rechte Winkel u. β1, β2, β3... = o; A u. A' ist der Druck, welchen die Aufhängepunkte erleiden. Es werden demnach folgende Gleichungen die Bedingung des Gleichgewichtes ausdrücken:

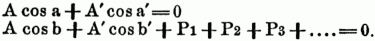
Ist T die Spannung irgend einer Seite dieses Polygons u. bezeichnen u u. v die Winkel, welche dieselbe resp. mit der horizontalen u. verticalen Achse macht, ferner p die Summe der Gewichte, welche vom Aufhängepunkte bis zum Endpunkte der Seite enthalten sind, so findet man die Gleichungen

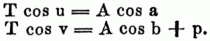
Die wichtigste Anwendung der Theorie des S-s ist die auf die Kettenlinie.