- Gleichung
Gleichung, 1) (Aequatio), die Zusammenstellung zweier gleicher Größen durch das Gleichheitszeichen, z.B. 6 + 4 = 2.5. Jede G. besteht aus zwei einander gleichen Theilen (Seiten, Membra aequationis), jeder aber kann aus mehreren Gliedern (Termini) bestehen. Es gibt zwei wesentlich verschiedene Arten von G-en. a) analytische od. identische G. sind solche G-n, bei denen, nöthigen Falls nach gehöriger Entwickelung, auf beiden Seiten des Gleichheitszeichens genau derselbe Größenausdrück steht; z.B. 4 = 4 od. 8 + 7 = 3.5 od. (a + b)2 = a2 + 2 ab + b2; sie müssen richtig sein, was auch die etwa in ihnen vorkommenden Buchstaben für Größen bedeuten mögen; b) algebraische od. Bedingungsgleichungen sind solche G-en, in denen nicht die eine Seite durch Entwickelung od. Umformung der anderen gebildet werden kann; z.B. 5 x = 40 od. a + y = b; sie müssen immer einen od. mehrere Buchstaben enthalten, welche einen ganz bestimmten Werth annehmen müssen, damit die G. richtig sei, u. man rechnet mit solchen G-en, eben um diesen Werth, welcher die Bedingungsgleichung zu einer identischen macht, zu finden. Man nennt dieses Geschäft das Auflösen der G. Diejenigen Buchstaben, welche jenen bestimmten Werth annehmen müssen, heißen die unbekannte od. gesuchte Größe, u. man wählt für sie immer einen der letzten Buchstaben im Alphabet x, y, z, u, v; die übrigen in der G. vorkommenden Größen heißen bekannte od. gegebene Größen u. sind entweder besondere Zahlen od. allgemeine, die dann durch die Buchstaben vom Anfang des Alphabetes bezeichnet werden. Das Auflosen der G. geschieht durch Umformungen der G., bei welchen fortwährend die Grundsätze zur Anwendung kommen: Jede Größe ist sich selbst gleich, Gleiches + gibt Gleiches, Gl. – Gl. gibt Gl., Gl. × Gl. gibt Gl., Gl.: Gl. gibt Gl. Hierdurch sucht man zu einer solchen Form der G. zu gelangen, daß die unbekannte Größe allein auf der einen Seite u. auf der anderen Seite in Verbindung von nur bekannten vorkommt; z.B. aus 5 x – 6 = 29 folgt 5 x – 35 u. hieraus x – 7. Der so gefundene Werth der Unbekannten heißt die Wurzel der G. In der Auflösung der G-en macht es einen wesentlichen Unterschied, ob die unbekannte Größe in der ersten, od. zweiten od. dritten etc. Potenz dabei vorkommt; man unterscheidet hiernach G-en von dem ersten, vom zweiten, vom dritten etc. Grade; man nennt diese G-en dann einfache u. zusammengesetzte, diese sind quadratische, kubische, biquadratische u. höhere G-en. Man kann die G-en, welche aufgelöst werden sollen, auf zweierlei Formen bringen, entweder man ordnet die Glieder, welche die unbekannte Größe enthalten, nach den Potenzen derselben u. bringt diese auf die eine Seite, das Bekannte aber auf die andere Seite,[402] od. man bringt alle Glieder der G. auf eine Seite, so daß auf der anderen 0 steht (man sagt hierfür kurz, die G. sei auf Null gebracht). Die allgemeine Darstellung dieser beiden Formen ist:
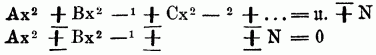
Sind die Coefficienten der unbekannten Größen bestimmte Zahlen, so heißt die von ihnen gebildete G. eine numerische od. Zahlengleichung, im Gegensatz zu der literalen od. Buchstabengleichung, in welcher die Coefficienten allgemeine Größen sind. Das Glied, welches mit keiner unbekannten Größe verbunden ist, heißt das absolute, ledige Glied. Eine G. heißt unvollständig, wenn einige Potenzen von der höchsten bis zur niedrigsten fehlen, im umgekehrten Falle vollständig. Kommt nur eine Potenz der Unbekannten vor, so heißt die G. rein, kommen mehrere vor, unrein od. zusammengesetzt od. gemischt. Die allgemeine Formel für die Auflösung einer G. vom ersten Grade mit einer unbekannten Größe von der Form Ax ± B = 0 ist x = ?B/A. Hat eine G. folgende Form: A2 = B, so heißt sie eine Exponentialgleichung, weil die unbekannte Größe in einem Exponenten vorkommt, od. auch logarithmische G., weil sie nur durch Logarithmen auflösbar ist, dann ist x = log. B/log. A. Sind mehrere Unbekannte vorhanden, so werden durch Elimination alle außer einer weggeschafft. Bes. drei Wege schlägt man hierbei ein, die Substitutions-, Combinations-, Subtractionsmethode (s.d. a.). Die allgemeine Form einer geordneten quadratischen G. ist: ax2 + bx + c = 0 hieraus:
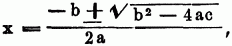
woraus erhellt, daß jede quadratische G. zwei Wurzeln haben muß, die reell u. ungleich sind, wenn das bekannte Glied c negativ ist; ist es dagegen positiv, wie in der angenommenen allgemeinen Form, so sind die beiden Wurzeln reell u. ungleich od. reell u. gleich, od. imaginär, je nachdem b2 >, =, < 4ac ist. Fourier hat eine auf einfache Division gegründete Methode zur Auflösung der quadratischen numerischen G-en gegeben, die sich aus folgender Form x = c/b + x ergibt, in welcher man die geordnete quadratische G. x2 + bx – c = 0 darstellen kann. Was die höheren G-en betrifft, so sind bes. folgende Punkte, auf welche es ankommt: a) durch Umformung derselben, ein od. mehrere Glieder, gebrochene Coefficienten, gebrochene Exponenten wegzuschaffen etc.; b) die allgemeinen Eigenschaften derselben in Beziehung auf ihre Wurzel anzugeben. Hierher gehört der Satz, daß jede geordnete G., deren Unbekannte x ist, sich durch x – a für jeden Werth von x theilen läßt, wenn a eine Wurzel derselben ist; ferner, daß jede G. so viele Wurzeln habe, als der Grad der G. Einheiten enthält; ferner der berühmte Cartesische Lehrsatz, daß eine G. nicht mehr positive Wurzeln habe, als es Zeichenwechsel, u. nicht mehr negative Wurzeln habe, als es Zeichenfolgen in der auf drei gebrachten Form der G. gibt, wobei man unter Zeichenwechsel u. Zeichenfolge den Umstand versteht, daß zwei auf einander folgende Glieder verschiedene od. gleiche Vorzeichen haben: c) die Grenzen der reellen Wurzeln der G. anzugeben; d) die Bestimmung der rationalen u. irrationalen Wurzeln der Zahlengleichung; e) die Auflösuug der allgemeinen G-en des dritten u. vierten Grades. Allgemeine G-en von einem höheren als dem vierten Grade aufzulösen, ist bis jetzt noch nicht gelungen. Durch Thom. Harriot, Joh. Hudde, Newton, de Lagny, Euler, Bezout (s.d. a.) u.a. sind nach u. nach die Mittel zur Auflösung numerischer G. entdeckt worden; s.u. Algebra u. Lagrange, Théor. de la résol. des équat. numériques, Par. 1808; Fourier, Analyse des equat. déterminées, ebd. 1841; Drobisch, Grundzüge der Lehre von den höheren numerischen G., Lpz. 1834; Budan, Nouvelle méthod. pour la résol. des équat. numér. etc., Par. 1807; Stern, Theorie der Kettenbrüche, Berl. 1834; Eytelwein, Anleitung zur Auflösung der höheren numerischen G-en, ebd. 1837; Heger, Auflösungsmethode für algebraische Buchstabengleichungen, Wien 1856. 2) (Astron.), ein gewöhnlich mit constanten numerischen Coefficienten versehener analytischer Ausdruck für eine solche Correction, durch welche die mittlere Bewegung irgend eines Himmelskörpers, z.B. eines Planeten, auf die wahre Bewegung ganz od. doch wenigstens zum Theil zurückgeführt wird; um z.B. für einen Planeten von kleiner Excentricität e aus der mittleren Anomalie m, d.i. derjenigen, welche er haben würde, wenn er sich mit gleichförmiger Geschwindigkeit in einem Kreise um die Sonne bewegt, die wahre od. elliptische zu finden, so hat man die erstere um 2 e sin m zu vermehren. Einer jeden G. dieser Art liegt die Kenntniß von der Größe der Einwirkung der verschiedenen Kräfte, durch welche die mittlere od. gleichförmige Bewegung in die wahre od. ungleichförmige übergeht, zum Grunde. Die G-en sind daher für den Calcul der physischen Astronomie wichtig. Gleichung des Mittelpunktes ist der Unterschied zwischen der mittleren u. wahren Anomalie od. die Differenz zwischen dem mittleren u. wahren Orte eines Planeten od. Kometen. Deshalb heißt die wahre Anomalie auch die coäquirte Anomalie. Die G. des Mittelpunktes kann positiv u. negativ Null u. ein Größtes werden; das Zu- u. Abnehmen derselben steht mit der Ungleichförmigkeit der heliocentrischen Bewegung in genauestem Zusammenhange. G. der Bahn, der Unterschied der wahren u. mittleren Anomalie (s.d. 6). E. der Zeit ist der Unterschied zwischen der mittleren u. wahren Sonnenzeit.
Pierer's Lexicon. 1857–1865.
