Quadratur

Quadratur, 1) (Astr.), so v.w. Geviertschein, s. u. Aspecten 4); 2) (Tetragonismus), Verwandlung einer Fläche in eine ihr gleiche Ebene von bekannter Gestalt. Sind die Flächen gekrümmt, so nennt man jene Operation oft Complanation (s.d.), welche der analytischen Geometrie angehört u. mittelst der Differentialrechnung ausgeführt wird. Das Quadrat hat man deshalb gewählt, weil man zur Herstellung desselben blos einer geraden Linie bedarf u. sich am leichtesten Vielfache eines solchen in übersehbarer Form construiren lassen. Ebene, geradlinige Figuren in ihnen gleiche Quadrate zu verwandeln, lehrt die Elementargeometrie. Die Aufgabe die von krummen Linien begrenzten Flächen zu berechnen (Q. der Curven) wird in der höheren analytischen Geometrie gelöst; ist eine ebne Curve durch die Gleichung y = f(x) zwischen rechtwinkligen Coordinaten gegeben, so ist die von der Abscissenachse, den beiden zu x = a u. x = b gehörigen Ordinaten u. dem zwischen diesen Ordinaten liegenden Bogen der Curven begrenzte Fläche

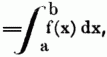
vorausgesetzt daß der Bogen zwischen den beiden Ordinaten die Abscissenachse nicht schneidet u. daß y zwischen diesen Grenzen nicht ∞ wird. Vgl. Verwandlung geradliniger Figuren. 3) Q. des Kreises. Da der Kreis einem Dreiecke, welches zur Höhe den Halbmesser u. zur Grundlinie die Peripherie desselben, u. der Kreisausschnitt einem Dreiecke von derselben Höhe gleich ist, das zur Grundlinie die Länge des zugehörigen Bogens hat, so ergibt sich, daß die Q. des Kreises gefunden ist, wenn man seinen Umfang durch den Halbmesser ausdrücken kann, d.h. daß die Q. des Kreises von der Rectification seines Umfangs u. umgekehrt abhängt. Von jeher ist diese Aufgabe von den Mathematikern bearbeitet worden. Archimedes vergleicht zuerst den Umfang des Kreises mit seinem Durchmesser, indem er ihn in regelmäßige Vielecke u. so bei einem 96 Eck die Peripherie zwischen die Grenzen 3¹/₇ u. 3¹⁰/₇₁ einschloß, wenn der Durchmesser = 1 genommen wird (vgl. Grenze). Hieraus ergibt sich das Verhältniß: der Durchmesser zur Peripherie = 7: 22. Eine kritische Aufgabe des Archimed. Werks ist mit Euteknios Commentar in Wallis Werken 3. Bd. enthalten. Peurbach (im 15. Jahrh.) erwähnt, daß Einige das Verhältniß zwischen denselben Stücken = 20000 : 62832 angeben. Vieta (1579) setzt den Durchmesser = 1 u. hat für die Peripherie gefunden 3,1415926535_..... Seine Rechnung ist enthalten in Vieta, Varia opera mathematica, in quibus tractantur Canon mathematicus etc., Par. 1609. Ludolph von Ceulen (1619) hat die Peripherie bis zur 32. Decimalstelle berechnet, mit ihm stimmt Vieta bis zur 10. überein. Man nennt die Zahl π, welche er gefunden, nach ihm die Ludolphische Zahl. In den gewöhnlichen Rechnungen reicht es aus, 7 Decimale zu nehmen, häufig werden ihre Logarithmen gebraucht; diese sind log. nat. π = 1,447298_..... so jedoch, daß wenn man bei der 7. Decimalstelle abbricht, die 8 in 9 verwandelt werden muß; log. vulg. π = 0,49714987_..... Lagny (st. 1734) berechnete diese Zahl bis auf 127 u. Georg von Vega (st. 1802) bis auf 140 Stellen u. fand somit: π = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09385 46095 50582 26136. Die 113. Decimale heißt bei Lagny u. vielen späteren Schriftstellern 7, doch hat man später 8 als das richtige gefunden. Behält man blos die 34 ersten Bruchziffern von π bei, verwandelt π in einen Kettenbruch u. sucht die Näherungswerthe desselben, so erhält man mit immer steigender Genauigkeit folgende Annäherungen an das Verhältniß des Durchmessers zum Umfange: 1: 3; 7: 22; 106: 333; 113: 355; 33102: 103993 etc.; die letzte ist 17929 30847 13965 674: 56326 58377 76847 017. Diese Verhältnisse geben der Reihe nach vom zweiten an eine Genauigkeit auf 2, 4, 6, 0,_... 34 Bruchziffern in dem Verhältniß von 1: π. Das vierte, 113 : 355, welches sich leicht im Gedächtniß behalten läßt, weil es auf regelmäßige Weise mit den drei ersten ungeraden Zahlen geschrieben wird, u. welches von des Adrian Metius Vater anderweitig gefunden, ist für den gewöhnlichen Gebrauch vollkommen ausreichend. Von der großen Genauigkeit des obigen vielstelligen Ausdrucks kann man sich eine Vorstellung machen, wenn man bedenkt, daß, wenn man bei der 10. Stelle abbricht u. dabei die letzte 5 in eine 6 verwandelt, der dabei begangene Fehler für einen Kreis von der Größe des Erdumfangs noch nicht die Breite eines Sandkörnchens beträgt, deren 100 auf einen Zoll gehen; das Verhältniß des Metius in einen Decimalbruch verwandelt weicht vom wahren Werthe von π erst in der 7. Decimale ab u. würde bei einem Kreis vom Umfang der Erde nur einen Fehler von 10 Fuß geben. Da jedes dem Kreise eingeschriebene Vieleck kleiner, jedes umschriebene aber größer ist als dieser; da ferner die Flächen der eingeschriebenen regulären Vielecke zunehmen, wenn man die Zahl der Seiten verdoppelt, die umschriebenen aber unter denselben Bedingungen abnehmen, u. da man durch fortgesetzte Verdopplung der Seitenzahl eines innern u. äußern Vielecks auf zwei gleichvielseitige kommen kann, deren Unterschied kleiner ist, als jede noch so kleine gegebene Fläche, so hat man nur nöthig, diese Vielecke durch das Quadrat des Halbmessers auszudrücken, um den Inhalt des stets dazwischen fallenden Kreises mit einem Grade von Genauigkeit zu erhalten, als verlangt war. Wenn man nun bedenkt, was sich leicht zeigen läßt, daß q = √Pp u.

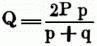
wo P den Inhalt eines umschriebnen, p den eines eingeschriebnen regelmäßigen nEcks,[731] u. Q u. q bezüglich den eines umschriebnen u. eingeschriebnen 2 nEcks bedeuten, so erhält man durch fortgesetzte Verdopplung der Seitenzahl u. Rechnung nach den Formeln, wenn man vom regelmäßigen Viereck (Quadrat) beginnt u. den Halbmesser = 1 setzt, folgende Tabelle:

_Seitenzahl des	___ Inhalt	___ Inhalt
__regelmäßigen	___ __des	___ __des
Vielecks in u. um	eingeschriebnen.	umschriebnen.
___ den Kreis.
4	2,0000000	4,0000000
8	2,8284271	3,3137085
16	3,0614674	3,1825978
32	3,1214451	3,1517249
64	3,1365484	3,1441183
128	3,1408311	3,1422236
256	3,1412772	3,1417503
512	3,1415138	3,1416321
1024	3,1415729	3,1416025
2048	3,1415877	3,1415951
4096	3,1415914	3,1415932
8192	3,1415923	3,1415928
16384	3,1415925	3,1415927
32768	3,1415926	3,1415926

Der zwischen das innere u. äußere 32768eck fallende Kreis ist mithin = 3,1415926. r², der begangne Fehler beträgt weniger als ein Zehnmilliontel vom Quadrat des Halbmessers, u. es ist dadurch der halbe Umfang für den Halbmesser = 1 bis 7 Bruchstellen genau gefunden. Man bezeichnet diese Zahl allgemein mit π. Auch durch geometrische Constructionen hat man jenes Verhältniß, od. zunächst eine gerade Linie finden wollen, welche dem Umfange eines Kreises gleich ist, od. wenigstens möglich nahe kommt. Die interessantesten sind folgende. E. G. Fischer (Lehrbuch der ebenen Geometrie, Berl. 1820 S. 271) gibt eine Construction an, nach welcher sich durch Fortsetzung einer u. derselben Operation eine Gerade finden läßt, welche sich einem Kreisbogen ohne Ende nähert, welcher kleiner als der halbe Umfang ist. Georg Behm, Kraft, Molther, Kochanski, Vieta, Crelles Journal der Mathematik 3. Bd. 4. Heft geben verschiedene meist sehr kurze u. einfache Constructionen an, durch welche man geradte Linien findet, welche vom Umfange des Kreises nach Verhältniß des gegebenen Kreises nur wenig, gewöhnlich erst in der vierten Decimale abweichen. Daß die Erfolge in Ansehung der Bemühungen nicht belohnender bei Lösung dieser Aufgabe erscheinen, ist nicht zu verwundern, wenn man, wie jetzt erwiesen ist, weiß, daß zwischen einem von zwei Coordinaten u. dem von diesen abgeschnittnen Bogen begrenzten Kreisstücke u. zwischen einer dieser Coordinaten, wenn sie willkürlich ist, keine algebraische Gleichung stattfindet, d.h. daß die unbestimmte Q. unmöglich ist. Doch sind bestimmte Stücke der Kreisfläche bekannt, welche sich allerdings streng quadiren lassen, nämlich die von eine Halbkreis mit dem Halbmesser r u. einem durch die Endpunkte des Durchmessers gelegten Quadranten eines Kreises vom Halbmesser r√2 begrenzte mondförmige Fläche, od. allgemeiner die sogenannte Lunulae des Hippokrates, s.d. Auch das ist jetzt aus den Eigenschaften der Kettenbrüche dargethan, daß die Zahl π (u. auch ihr Quadrat) eine Irrationalzahl ist. Ob aber nicht π die Wurzel einer algebraischen Gleichung mit einer endlichen Anzahl von Gliedern sei, d.h. einer solchen, wo die Coëfficienten sämmtlich rationell sind, scheint schwer zu beweisen zu sein. Von Lacroix ist ein Beweis, daß die Q. des Kreises überhaupt unmöglich ist, in der neuen Ausgabe von Montucla, Histoire de la quadrat du cercle, aufgestellt worden. Die gegenwärtige Analysis bedient sich zur Berechnung der Zahl π der für arc sin, arc cos., arc tg. aufgestellten nach den Potenzen der zugehörigen sin, cos etc. fortschreitenden Reihen, in welchen man den zum Halbkreis gehörigen Werth der betreffenden goniometrischen Functionen einsetzt, u. zwar ist diese Methode weit bequemer als die oben geschilderte von den regelmäßigen Vielecken ausgehende; z.B. geht aus der Reihe für arc sin hervor

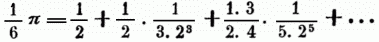
od. aus der Reihe für arc tg. findet sich ¹/₄ π als Summe zweier sehr schnell convergirender Reihen, nämlich:

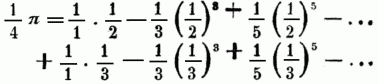
Lagny war der erste, welcher durch derartige Reihen π berechnete (Mém. de l'Acad. 1719, S. 144). Die genaue Lösung der Aufgabe an sich betrachtet ist im Ganzen von keinem bedeutenden Nutzen, da wir uns mit den bekannten Näherungswerthen vollkommen begnügen können. Und wenn Mathematiker aller Zeiten sich damit beschäftigt u. dabei oft die wunderlichsten u. unsinnigsten Resultate gefunden haben, welche sie der Anerkennung würdig hielten, so sind doch auch auf der andern Seite manche Wahrheiten u. interessante Sätze dabei aufgefunden worden, welche die Wissenschaft bereichert u. den Scharfsinn einzelner tüchtiger Arbeiter beurkundet haben. Vgl. Montuclas, Histoire des recherches sur la quadrature du cercle; außerdem geben die Lehrbücher der analytischen Geometrie, so wie zum Theil der Differentialrechnung die Quadraturen.